(Read in English)

Друзі, це така цікава тема про основні рівняння електродинаміки, одне з яких можна записати як індукцію і змінити наше уявлення про те, що відбувається в електричному колі.

---

2.5.2. Рівняння Максвелла

Дж. К. Максвелл записав свої геніальні рівняння в 1865 р. Рівняння Максвелла - це фундаментальні рівняння елек­тродинаміки, які описують електромагнітні явища в будь-якому середовищі. Вони узагальнюють експериментальні і теоретичні праці фізиків першої половини XIX ст. і, насам­перед, дослідження М. Фарадея. Основні закони електроди­наміки Максвелл сформулював у вигляді чотирьох рівнянь, які подамо в інтегральній формі, як в найбільш простій і наочній.

Перше рівняння Максвелла спирається на закон Біо-Савара-Лапласа та поняття струму зміщення. Виділимо в провіднику, в якому існує змінний струм, довільну площад­ку обмежену контуромТоді

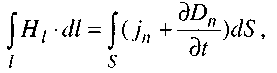    (2.88)    

де - проекція вектора напруженості магнітного поля на напрям дотичної до контурау даній точці,- нормальна до вибраної площадки складова густини струму провідності, - нормальна до площадки складова вектора електричної індукції. Тут вжита частинна похідна dD/dt, щоб врахувати факт залежності D як від часу, так і від про­сторової координати. Струм зміщення виникає лише тоді, коли D змінюється з часом. Це рівняння показує, що магнітне поле вихрове і що воно виникає незалежно від на­явності постійних магнітів. Виникнення магнітного поля зумовлене двома факторами: рухом електричних зарядів (струм провідності) і зміною в часі електричного поля (струм зміщення).

Друге рівняння відображає закон електромагнітної індукції Фарадея:

ЕРС, як відомо, дорівнює роботі сторонніх сил по пе­реміщенню одиничного заряду, тобто тому матимемо

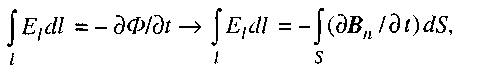 (2.89)

де — проекція вектора напруженості електричного поля на напрям дотичної до контура у даній точці, - нормальна до поверхні складова вектора магнітної індукції. З цього рівняння видно, що крім електростатичного поля в природі існує електричне поле, джерелом якого є змінне магнітне поле. Всяка зміна електричного поля зумовлює появу змінного магнітного поля, лінії напруженості якого замк­нені і охоплюють лінії електричного поля (перше рівняння); всяка зміна магнітного поля зумовлює появу змінного електричного поля, лінії напруженості якого замкнуті й охоплюють лінії магнітного поля (друге рівняння).

Третє рівняння Максвелла показує, що джерелом електричного поля є електричні заряди:

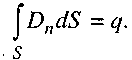
Ліва частина цього рівняння - потік вектора індукції електричного поля через замкнену поверхню площею 5.

Четверте рівняння відображає факт відсутності маг­нітних зарядів. Повний потік вектора магнітної індукції В через замкнену поверхню площею S дорівнює нулю:

---

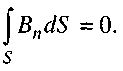
Наведені рівняння Максвелла не враховують будову речовини і взаємодію електромагнітного поля з частинками речовини. Вплив середовища на електромагнітне поле за­дається через його електропровідність, а також діелектрич­ну ε і магнітнупроникності. Тому до рівнянь Максвелла слід додати ще три рівняння, які називаються матеріальни­ми:

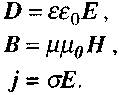
Рівняння Максвелла описують величезне коло явищ (електродинаміка, оптика, електротехніка, радіотехніка, ас­трофізика, фізика плазми тощо). Теорія Максвелла не тільки пояснила вже відомі факти, а й передбачила нові і важливі явища. Абсолютно новим у цій теорії було припу­щення Максвелла про магнітні поля струмів зміщення. На основі цього припущення Максвелл предбачив існування електромагнітних хвиль, тобто змінного електромагнітного поля, яке поширюється в просторі з певною швидкістю. Теоретичне дослідження властивостей електромагнітних хвиль привело згодом Максвелла до створення електро­магнітної теорії світла. Пізніше експериментальне вдалося отримати електромагнітні хвилі і провести досліди, які бли­скуче підтвердили електромагнітну теорію світла, а з нею і всю теорію Максвелла.

---

Коротка історія ЕМ (для чайників)

«Трактат про електрику і магнетизм» Максвелла був опублікований в 1873 році. Його 1000-сторінкова книга містила 20 рівнянь. Для візуалізації та розуміння власних математичних ідей ЕМ він використовував механічні аналогії: кульки, підшипники, гаки. ... Генріх Герц (1888) звільнив теорію ЕМ від механічної моделі. ... Олівер Хевісайд (1893) модернізував теорію ЕМ, скоротивши рівняння до чотирьох, надавши їм форму, загальновживану сьогодні. … У 1905 році теорія Максвелла стала основоположним елементом для спеціальної теорії відносності (СТВ) Ейнштейна.

Перше рівння Максвелла огляд від ШІ :

Рівняння Максвелла, включаючи закон Ампера, описують електромагнітні поля та його взаємозв'язок з електричними зарядами та струмами. Закон Ампера в інтегрованій формі свідчить: ∮B · dl = μ₀(I + ε₀ dΦE/dt), де B - індукція магнітного поля, dl - елемент довжини контуру, μ₀ - магнітна постійна, I - сила струму, ε₀ - електрична постійна, ?
У чому суть закону Ампера:
Закон Ампера передбачає, що магнітне поле створюється електричними струмами і електричними полями, що змінюються (струмом зміщення). Він зв'язує лінії магнітного поля, що утворюють замкнутий контур, із струмами, які протікають через площу, обмежену цим контуром.
Зміни Максвелла:
Спочатку закон Ампера не враховував зміни електричного поля у часі. Максвел вніс поправку, ввівши поняття "струм зміщення", яке враховує зміну електричного поля в конденсаторах. Цей струм усунення робить закон Ампера більш повним і точним, описуючи магнітні поля, що виникають за змін електричного поля.
Коротко і зрозуміло:
Закон Ампера в рівняннях Максвелла стверджує, що магнітне поле генерується струмами і електричними полями, що змінюються. Це означає, що якщо струм протікає провідником або змінюється електричне поле (наприклад, в конденсаторі), то в його околиці створюється магнітне поле. Максвелл розширив закон Ампера, включивши до нього поняття " струм зміщення " , що робить його повнішим і дозволяє описувати магнітні поля, які під час змін електричного поля.

Розглянемо магнітне поле яке утворюється навколо провідника зі струмом. Закон Біо-Саварда був опублікований в 1820 році (за 11 років до відкриття ЕМІ Фарадеєм у 1831 році), рівняння Максвелла вперше були опубліковані в 1861 році, тому розглянемо цій закон:

Магнітне поле навколо прямолінійного провідника за законом Біо-Савара: 

B = kI / 2r ,  одиниця виміу Тесла, (магнітна індукція)
або  Н = I / 2πr  одиниця виміу Ампер на метр; (маннітна напруженність)

 мал. 1

де B — магнітна індукція в точці М на відстані r від прямолінійного провідника із струмом I (мал. 1); k — коефіцієнт пропорційності, величина і розмірність якого залежать від вибору системи фізичних величин, r — радіус-вектор.
У Міжнародній системі величин (ISQ) k = μ0 / 4π,де  μ0 — магнітна стала.  У гаусовій системі   k = 1 / с,   де c — швидкість світла.

Закон Біо-Савара-Лапласа — це фундаментальний закон електромагнетизму, який описує зв'язок між електричним струмом і магнітним полем, яке він створює. Він дає змогу розраховувати характеристики магнітного поля для провідників довільної конфігурації. Закон стверджує, що магнітна індукція в точці простору пропорційна величині струму і обернено пропорційна квадрату відстані від провідника. Цей закон також аналогічний закону Кулона в електростатиці, де справедливий принцип суперпозиції для магнітних полів.

Закон Ампера — закон взаємодії постійних струмів, котрий установив Андре-Марі Ампер 1820 року. Із закону Ампера виходить, що паралельні провідники з постійними струмами, які течуть в одному напрямі, притягуються, а в протилежному — відштовхуються. Законом Ампера називають також закон, що визначає силу, з якою магнітне поле діє на невеликий відрізок провідника зі струмом (сучасна формула далі).

Закон взаємодії двох елементарних електричних струмів, відомий як закон Ампера, насправді пізніше запропонував Герман Грассман (тобто його було б правильніше називати законом Грассмана).

.

Максвелл запропонував найзагальнішу форму закону взаємодії двох елементарних провідників зі струмом, у якій є коефіцієнт k (його не можна визначити без деяких припущень, що ґрунтуються на дослідах, у яких активний струм утворює замкнутий контур)^[3]:

У власній теорії Ампер узяв k = −1, Гаус прийняв k = +1, як Грассман і Клаузіус. У неефірних електронних теоріях Вебер прийняв k = −1, а Ріман прийняв k = +1. Ріц у своїй теорії залишив k невизначеним.

Для сили взаємодії двох замкнутих контурів C1 і C2 з k=+1 виходить стандартний вираз.

Але що ми бічимо, виникнення магнітногї індукції навколо провідника зі струмом встановленно законом Біо Савара Лапласа .  Закон Ампера  (та подібні тлумачення) визначають дію двох провіднікив зі струмом та з якою силою вони це роблять. Раніше таку залежність було встановленно для електричних зарядів.   Зако́н Куло́на — один з основних законів електростатики, який визначає величину та напрямок сили взаємодії між двома нерухомими^[1] точковими зарядами. Експериментально з задовільною точністю закон вперше встановив Генрі Кавендіш у 1773. Він використовував метод сферичного конденсатора, але не опублікував своїх результатів. У 1785 році закон був встановлений Шарлем Кулоном за допомогою спеціальних крутильних терезів .  Закон Ампера (для двох провідників зі струмом) тотожний Закону Кулона (для двох електричних зарядів).

Закон Кулона:    Закон Ампера : 

Причина за якою видбувається дія виникнення магнітної індукції не розкрита. Рух електричних зарідів якій спонукає прояву явіща магнітної індукції дуже не визначенне тлумачення. Звідки з'явилося тлумачення струму окремого від напруги.  Це тлумачення ввів Георг Ом. У 1825—1827 роках  він проводив досліди з джерелом ЕРС у вигляді термопари, гальванометром і металевим дротом. Він виявив, що сила струму через дріт у його дослідах добре описується лінійним законом на основі трьох параметрів, і в 1827 опублікував результати у вигляді роботи Die galvanische Kette, mathematisch bearbeitet. Досліди Георга Ома проводилися до зародження теорії ланцюгів і правил Кірхгофа (1845—1847), теорії електромагнітного поля (1864), рівнянь Максвелла (1861-1884) та теорії Друде (1900).  Більш точно — закон Ома стверджує, що сила струму у провіднику між двома точками (мал. 1) прямо пропорційна напрузі на цих двох точках. Вводячи константу пропорційності — опір [R], можна прийти до звичайного математичного рівняння, яке показує цю залежність   I = U / R.   Сучасна фізика пояснює виникнинне струму  переміщенням електричних зарядів. 

Си́ла електри́чного стру́му (сила струму або просто струм) — кількісна характеристика електричного струму в провіднику, скалярна величина I = Δq / Δt, яка відповідає кількості заряду (Δq), що проходить крізь переріз провідника за час (Δt), розділеному на цей проміжок часу. За одиницю сили струму беруть таку силу струму, за якої відрізки паралельних провідників довжиною 1 м, що розташовані на відстані 1 м один від одного, взаємодіють із силою 2·10⁻⁷ Н. Силою струму називають ще величину, що визначає швидкість перенесення заряду частинками, які створюють струм, крізь поперечний переріз провідника. Струм — це упорядкований рух заряджених частинок. У системі SI сила струму вимірюється в амперах (позначення А). Відповідно, густина струму вимірюється в A/м².  Якщо за кожен проміжок часу Δt заряд Δq  однаковий і напрямок струму незмінний, то такий струм називають постійним.     

Для класичної системи заряджених частинок із зарядом [ e ] безмежно малий заряд [ dQ ], що переноситься за час [ dt ] через елементарну площадку [ dS ], перпендикулярну до напрямку середньої швидкості v частинок визначається як: 

dQ = e*n*v*dS*dt, де e — заряд частинок, v — швидкість руху частинок, а n — їхня кількість в одиниці об'єму. Сила струму dI крізь площадку dS визначається співвідношенням     dI =e*n*v*dS,   звідки для густини струму:   -j = e*n*v  — густина електричного струму, де риска над символами є середнім показником.   

Тобто рух частинок єлектричного заряду е у відповідной кількісті n  на об'єм, зі швидкістю v,  через відповідний перетин провідника S   [ dI =e*n*v*dS  ] спияє виникненню явища магнітної індукції В ?   Які ознаки нам відомі у електричного та магнітного полів? 

Електричний заряд — фізична величина, яка характеризує здатність тіл створювати електромагнітні поля та брати участь в електромагнітній взаємодії. Електричний заряд звичайно позначають латинськими літерами q або великою буквою Q. Одиницею вимірювання електричного заряду в системі одиниць SI є кулон. Взаємодію електричних зарядів без врахування їх руху вивчає електростатика, а зарядів, що рухаються — електродинаміка. Рух електричних зарядів називається електричним струмом.  Є ще на що не звертають увагу і це Силова лінія  векторного поля — це уявна лінія в просторі, дотична до якої в будь-якій точці збігається з напрямком поля в цій точці.  Концепція силових ліній допомагає візуалізувати векторні поля в просторі.  Силові лінії перпендикулярні до еквіпотенціальних поверхонь.  Силові лінії електричного поля починаються в точках розташування позитивного заряду, або на нескінченності, і закінчуються в точках розташування негативного заряду, або на нескінченості.  Силові лінії магнітного поля починаються на полюсах магніту і ведуть до протилежних полюсів, ніколи не виходячи на нескінченність.  Силові лінії вихрового поля замкнуті.  Ці лінії малють а магнітні силові линиї візиалізірують, але це у фізиці всеодно уявна лінія. 

Електричне поле:        Магнітне поле:  

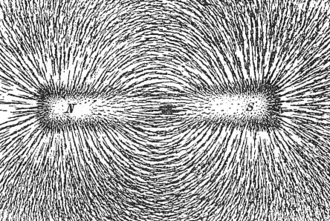
Далі маємо по факту три типу індукції у електормагетизмі: електростатичну, магнітну, та електоромагнітну.   

Електростати́чна індукція виникає, коли до тіла піднести інше заряджене тіло. Якщо в такому тілі існують вільні заряди, то вони перетікають з однієї частини тіла в іншу. Наприклад, при піднесенні достатньо зарядженого тіла до нейтрального тіла, від'ємно заряджені вільні електрони в нейтральному тілі перетечуть в частину тіла, розташовану ближче до додатного заряду, залишаючи далеку частину додатно зарядженою. Таким чином утворюється наведений заряд. Електростатична індукція виникає в провідниках, оскільки в них є вільні носії заряду. В діелектриках в електричних полях інших тіл виникає поляризація. Перетікання заряду в провідниках продовжується доти, доки електростатичний потенціал усіх точок провідника не стане однаковим, оскільки при рівності потенціалу електричні струми припиняються.  (Вимірювання не вказано у джерелі, але Електрична напруженність вимірюеться у вольт на метр   E = q / ε₀r²)

Це явіще зазнавено у рівняні Максвелла  D = ρ [∫DdS = q]  або  E = q / ε₀r², на Теорему Гаусса що джерелом електричного поля (напруженністі) є електричні заряди q .   Електричний заряд -  це фізична величина, яка характеризує властивість частинок і тіл вступати в електромагнітну взаємодію.  Тобто це рівень потенциалу одинично обїекту. Як цій зарял взаимодіє? вірно церз явіще Електростатичної індукціі або Електризації — це процес набуття макроскопічними тілами електричного заряду. 

Магнітна індукція (індукція магнітного поля) — векторна фізична величина, основна характеристика величини й напрямку магнітного поля. Сила дії магнітного поля на заряджені частинки й тіла, які мають магнітний момент і рухаються відносно даного магнітного поля. Вектор магнітної індукції зазвичай позначають латинською літерою B.  В системі SI магнітна індукція поля вимірюється в теслах (Тл). У системі СГС — в гаусах (Гс).

 До цього явища відноститься  дія намагнічування феромагнетиків - коли феромагнітний зразок поміщують у зовнішнє магнітне поле, домени, магнітні моменти яких зорієнтовані за напрямком цього поля, збільшуються за рахунок зменшення доменів з іншою орієнтацією магнітних моментів. Також відбувається частковий поворот магнітного моменту в кожному домені 

Електромагні́тна інду́кція — явище створення в просторі вихрового електричного поля змінним магнітним потоком. Одним із наслідків електромагнітної індукції є зв'язок між змінними електричним та магнітними полями в електромагнітній хвилі, інший наслідок, практично важливий для генерації електричного струму, — виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється. Одиниці вимірювання електромагнітної індукції — тесла (в системі СІ), гаус (у системі СГС); 1 Тл = 10⁴ Гс.* 

Але це тлумачення мені не подобається.  Поперше в данному випадку це створення або перетворення. Одиниці виміру повінна бути по кінцевому явіщу яке винікае, а винікає в цьому випадку електрорушийна сила .

Електрорушійна сила  — кількісна міра роботи сторонніх сил із переміщення заряду, характеристика джерела струму.  Позначається здебільшого літерою ℰ або Е, інколи стилізується як рукописна ε, вимірюється в системі SI у вольтах. Зазвичай електрорушійна сила скорочується в текстах до е.р.с. (ЕРС).  Електрорушійна сила ділянки кола дорівнює енергії, яку отримує одиничний заряд, пройшовши цю ділянку кола. Для замкненого кола, де f — стороння сила:

Явище електромагнітної індукції відкрив у 1831 році Майкл Фарадей. До того було відомо, що електричний струм у провіднику створює магнітне поле. Однак оберненого явища не спостерігалося. Постійне магнітне поле не створює електричного струму. Фарадей встановив, що струм виникає при зміні магнітного поля. Якщо підносити й віддаляти до рамки з провідного матеріалу постійний магніт, то стрілка підключеного до рамки вольтметра відхилятиметься, детектуючи електричний струм. Ще краще це явище проявляється, якщо вставляти (виймати) магнітне осердя в котушку з намотаним провідником.  

Вчений фізик Фарадей встановив кількісний закон електромагнітної індукції, описавши його рівнянням:  E=−N dΦ / *dt,  де  E — електрорушійна сила (ЕРС) у вольтах, яка виникає в котушці, що перебуває у змінному магнітному полі, у вольтах, N — кількість витків у котушці, Φ — магнітний потік у веберах.  Якщо в провіднику виникає електрорушійна сила, то відповідно, індукований в ньому струм буде визначатися за законом Ома формулою  I = E / R,  де R — опір провідника. Такий струм називається індукційним струмом.

___________________________________________

 

Продовження на сторінці за посиланням    Maxwell's equations 2

 

.