РезюмеПредлагается гипотеза: существует потенциальное поле центробежных сил инерции (ПЦСИ) как подсистема структуры элементов среды физического вакуума (ФВ, эфира). Поле центробежных сил это «потенциальная яма» энергии в которую масса объекта из вещества «падает бесплатно», также, например, как и в гравитационную «потенциальную яму». При совершении работы центробежными силами затрачивается (превращение из потенциальной в кинетическую) энергия ФВ, ПЦСИ, а не кинетическая энергия вращения массы маховика, которая остается неизменной. Более того, выполнение законов сохранения кинетической энергии вращения и момента импульса (количества движения) при изменении радиуса инерции вращающейся массы на орбитальной траектории обеспечиваются энергией, работой и силами ПЦСИ. В доказательство правомерности этих утверждений описываются устройства и проведение на них, так называемых, «решающих экспериментов» по получению даровой кинетической энергии (свободной энергии). Потенциальное поле центробежных сил инерцииРеальный физический эффект, силы инерции (вообще) — не «математический прием», введённый д'Аламбером, и они не «фиктивны». Конкретные силы инерции, центробежные силы инерции, также — не «фиктивны», и имеют ту же природу, что и силы других основных взаимодействий природы: гравитационного, электромагнитного (и электростатического, и магнитного). «Консервативными силами» силы гравитационные, электростатические, магнитные названы из-за того, что они принадлежат природным силовым полям с одноименными названиями; источником работы этих сил является потенциальная энергия поля, как подсистемы окружающей среды. В более широком плане научное открытие физического закона (предлагаемой гипотезы, принцип УЭПП) формулируется так: на изменение направления вектора импульса (количества движения массы) затрачивается работа внешних сил, которая деформирует структуру системы среды ФВ и на радиусе кривизны траектории движения массы (радиусе инерции) формирует вихрь элементов ФВ, искусственную механическую подсистему,потенциальное поле центробежных сил инерции, которая обладает свойствами квантово-механической системы. Мы предполагаем, что квантово-механические свойства этой макросистемы заключаются в том, что в вихре ФВ на радиусе инерции вращающейся массы квантуются ряд ее параметров: момент импульса массы вещества, плотность массы слоев элементов подсистемы ФВ по объему, а главное, скачком изменяется плотность энергии по объёму слоев элементов ФВ. Квантование плотности энергии среды ФВ в ПЦСИ приводит к появлению градиента потенциалов, что и является причиной образования центробежных сил инерции. В квантовании плотности кинетической энергии движения элементов эфира по объему в ПЦСИ (ОФМ по Иванову Б.П.), формирующем градиент потенциалов, заключается объяснение механизма образования сил и мощности работы всех потенциальных полей, например, гравитационного поля, электрического, магнитного, при фотоэффекте, в подъемных силах Архимеда и др., в том числе, и образование кинетического момента центробежных сил в потенциальном поле центробежных сил инерции. Доказать правомерность этих утверждений позволили проведенные мной, так называемые, «решающие эксперименты» по получению даровой кинетической энергии потенциального поля консервативных сил (свободной энергии) на базе изобретенных мной механических устройств: «Генераторе Богомолова (ГБ)» и «Генераторе Маринова-Богомолова (ГМБ)». ГБ получает непосредственно свободную энергию центробежных сил. ГМБ получает свободную энергию центробежных сил опосредовано, через физический эффект прецессии. Объяснение природы получения свободной энергии в ГБ и ГМБ возможно на базе новой парадигмы физики [5], постулирующей, что элементы вещества есть вихри [9] эфирной среды, находящиеся в состоянии равновесия энергообмена со средой. Эфирная среда (физический вакуум (ФМ)) имеет свойство самоструктурироваться и формировать свои элементы как механические системы (вихри, волновые пакеты стоячих волн) по универсальной кинематической схеме «организационная форма материи» (ОФМ по Иванову Б.П. [6]), в том числе объекты вещества, как комплекс систем ОФМ и, в том числе, формировать искусственные ОФМ, потенциальные поля центробежных сил инерции. Все ОФМ имеют свойства квантово-механических систем: квантование плотности кинетической энергии движения элементов эфира по объему, плотности массы, момента импульса на радиусе кривизны траектории вихря, радиусе инерции локализованной массы элементов эфира. Вечное движение, обмен энергией, ее превращения в среде принимаются априори, описываются универсальным алгоритмом действия, названным «закон взаимосвязи процессов (ЗВП)» [3]. Представления новой парадигмы физики позволяют изобретать и строить устройства, способные черпать свободную энергию из окружающей среды ФВ. Решающие экспериментыЦентробежный генератор Богомолова (ГБ)Схема центробежного генератора изображена на рис.1: На валу обратимой электрической машины (мотор-генератор) установлен центробежный регулятор скорости Уатта. При достижении определенной угловой скорости ω1вращающихся на валу грузов с общей массой m возникает центробежная сила инерции Fцб = m · ω12 · R1, которая совершает работу центробежных сил Aцб = F · R1, то есть разводит рычаги с грузами на максимальную величину радиуса кривизны траектории вращения R1 и при этом сжимает пружину. При этом электрическая машина работает в режиме «мотор» и, затрачивая некоторую мощность от батарей, превращает электрическую энергию в кинетическую. 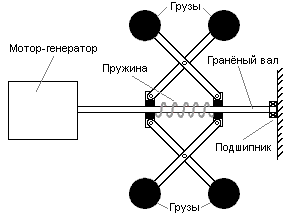 Рис.1. Во втором такте действия этой схемы машина работает как генератор. Уменьшение скорости вращения грузов ω1 приводит к расширению пружины и возвращению аккумулированной энергии Eк, которая преобразуется во вращающий момент вала генератора. Поясним это на примере: аналогично ускорению вращения фигуриста, руки которого подтягиваются к туловищу, в силу закона сохранения момента импульса (момент количества движения L = m · R2 · ω = const), работа взведенной в первом акте пружины по перемещению масс грузов m на радиусе кривизны R1 – R2 против центробежных сил Fцб, приведет к росту кинетической энергии W = 1/2 · m · R12 · ω12 – 1/2 · m · R22 · ω22 и росту угловой скорости этих грузов ω2 = m · R12 / (m · R22) Это и есть та энергия, которую пользователь получает «даром». При этом также ожидаются некоторые потери, в соответствии с характеристиками реальной применяемой электрической машины. В результате действия устройства за два такта, мы получим в конце второго такта приращение к возвращенной энергии, затраченной в первом такте, то есть приращение мощности устройства за счет свободной энергии среды физического вакуума (ФВ, эфира). Теоретически, согласно гипотезе автора [5], искусственная система вращения грузов формирует в структуре элементов среды физического вакуума подсистему, которой дано название «потенциального поля центробежных сил инерции» ПЦСИ (или организационная форма материи ОФМ по Иванову Б.П. [6]). Природа этого искусственного поля такая же, как и природа гравитационного, электростатического и магнитного полей. То есть ПЦСИ есть потенциальная яма энергии. В нее грузы «падают» так же «бесплатно» как человек в колодец, а чтобы выкарабкаться из нее необходимо совершить работу, например, работу мышц рук фигуриста. Источник приращения мощности устройства это «бесплатно» взведенная в первом акте пружина во время «падения» грузов в потенциальную яму энергии ПЦСИ. Если обратимая электрическая машина за два такта действия возвращает нам (за вычетом потерь) первоначальную энергию, то откуда же берется сила и энергетический потенциал искусственной ОФМ для взведения пружины? Кинетическая энергия вращения по инерции системы масс грузов накапливается (превращается из электрической) благодаря работе, совершаемой силами упругости рычагов по изменению прямолинейных тангенциальных векторов импульса (мгновенной орбитальной скорости) массы грузов на радиусе их инерциального движения. Источник мощности действия сил структурной целостности ВЕЩЕСТВА рычагов (сил Кулона, Ван Дер Вальса) находится в той же окружающей нас, вечно движущейся материальной субстанции, среде физического вакуума. Как показано в [6], каждая частица вещества — это подсистема физического вакуума, представляющая собой вихрь организационной формы материи локально концентрированных элементов субстанции эфира, можно сказать «аккумулированную энергию структуры среды». Данная энергия и является причиной дополнительной деформации структуры физического вакуума, а значит и образования нового энергетического потенциала искусственного поля инерции центробежных сил вокруг вещества грузов, при условии наличия вращения грузов. Эксперимент по использованию центробежной силы для получения свободной энергииУпрощенная схема эксперимента известна, как «маятник Максвелла» (рис.2). Это диск, насаженный на горизонтальную ось, к которой привязаны две нити. Их верхние концы закреплены на перекладине. 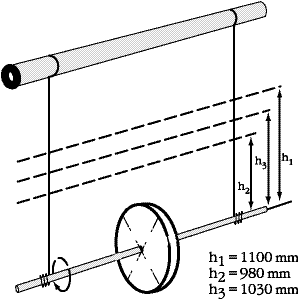 Рис.2. Если закручивать нити вокруг оси, то диск поднимается на высоту h и запасает потенциальную энергию гравитационного поля Земли Е = m · g · h (где m – масса маховика; g – ускорение свободного падения; h – высота падения массы). Если мы отпустим маятник, то начнутся периодические затухающие колебания «вниз-вверх»: сначала нить раскручивается и потенциальная энергия превращается в кинетическую энергию вращения диска; дойдя до нижней точки и продолжая по инерции вращаться, диск поднимается вверх, утилизуя кинетическую энергию вращения и превращая ее вновь в потенциальную. Это устройство интересно тем, что, в силу закона сохранения энергии, наглядно и точно мы можем наблюдать утилизацию кинетической энергии вращения маховика, измеряя только параметр h, высоту подъема по нитям маховика во втором полупериоде колебания, в сравнении с выстой, с которой маятник начал падение в первом полупериоде. Разность h1 – h2 за два полупериода колебания прямо пропорциональна потерям кинетической энергии вращения на работу аэродинамического сопротивления и трение. В нашем эксперименте мы усложнили «маятник Максвелла», заменив диск маховика на центробежный регулятор скорости Уатта, в соответствии с его описанием в статье [2}. Его основное отличие от маховика Максвелла в том, что момент инерции маховика изменяется работой центробежных сил при перемещении грузов (общая сумма весом 1200 г) на рычагах из положения минимального радиуса 40 мм до максимального 90 мм. При этом рычаги сжимают пружину с силой около 16 кг. Опыты проводились в три этапа. На первом мы экспериментально установили необходимую высоту подъема 1100 мм при закручивании нитей на ось, падение маховика с которой обеспечивает достижение такой скорости его вращения и развивает такую центробежную силу, которая обеспечивает разведение грузов на величину максимального радиуса 90 мм и полное сжатие пружины. На втором этапе грузы зафиксировали на минимальном радиусе 40 мм, тем самым выключив работу центробежных сил по сжатию пружины, и замерили потери кинетической энергии на аэродинамическое сопротивление и трение деталей. В таком виде маховик поднялся на высоту 980 мм, потеряв 120 мм. На третьем решающем этапе убрали фиксатор грузов и включили в работу центробежные силы. Как и на втором этапе, центробежный регулятор скорости Уатта начал падать, раскручиваясь с высоты 1100 мм, сжал пружину и поднялся на высоту 1030 мм, то есть превысил высоту второго этапа на 50 мм! Выводы автора по результатам эксперимента: - На третьем этапе маховик преодолел высоту «потерь» h = 980 мм. Это значит, что пружина была сжата для нас «бесплатно».
- На третьем этапе маховик превратил кинетическую энергию в потенциальную, поднялся на дополнительную высоту 50 мм. Это значит, что в соответствии с законом сохранения момента количества движения, внешняя сила энергии сжатой пружины совершила работу по изменению момента количества движения вращающихся масс, придав дополнительное ускорение маховику, увеличив его кинетическую энергию «бесплатно»!
- Для практического использования в промышленном варианте генератора Богомолова для получения свободной энергии необходимо достигать высокой угловой скорости, более 10 тыс. об/мин и совершать работу центробежных сил по перемещению вращающейся массы на желательно меньшую разность радиусов инерции.
Описанная в статьях схема центробежного регулятора не является достаточно прочной для мощных экспериментов. Для промышленного генератора автор предлагает схему устройства на гидравлическом принципе работы и пневматической пружине (ноу-хау).Прецессионный генератор свободной энергии. Описание экспериментовФизический эффект прецессии — один из многих инструментов, предоставленных человечеству Природой для получения свободной энергии. Он является ключом к неиссякаемым кладовым консервативных сил потенциальных полей. Академическая физика уже много лет замалчивает этот факт. В массовых тиражах справочников для инженеров и студентов вы не найдете выводов о том, что мощность на валу момента сил прецессии гироскопа является даровой энергией, возникающей в результате действия таких внешних сил, приложенных к оси ротора, как, например, гравитационная энергия силы веса смещенного центра масс ротора, а отнюдь не благодаря превращению электрической энергии, питающей ротор гороскопа, в механическую. Учебник 1964 года [3] кратко знакомит с теорией гироскопов лишь узкий круг посвященных в тайны ФЭП, будущих инженеров-авиастроителей, прежде чем им предстоит изучать схемы и конструкции авиационных гироскопов. На основании богатого многолетнего опыта проверки математической теории на практике, Д.С.Польпер делает вывод: «Нутационное движение гироскопа является движением по инерции... Избыточный инерционный момент, который в теоретической механике называется центробежным моментом сил инерции, стремится совместить ось ротора гироскопа с осью наружной рамки кардана, т.к. равновесие при нутации оказывается нарушенным. В процессе прецессионного движения устанавливается динамическое равновесие между моментом внешних сил и гироскопическим моментом, равным моменту центробежных сил... Гироскопический момент и есть то инерционное сопротивление, которое оказывает гироскоп приложенному к нему моменту внешних сил... Из уравнения закона прецессии следует, что прецессионное движение оси ротора гироскопа определяется моментом внешних сил, действующих на гироскоп и равно ему... Прецессионное движение является движением без инерции». Заканчивая цитату, сделаем наш собственный акцент из выводов автора: прецессионное движение — это специфический инструмент, позволяющий использовать энергию внешних сил, приложенных к ротору гироскопа благодаря возникающему при ФЭП моменту центробежных сил инерции. В учебнике выводятся формулы законов движения гироскопа на механических моделях, где в качестве внешней силы приложенной к оси ротора используется вес гири, то есть сила энергии гравитационного поля, мощность которого в виде момента сил прецессии утилизуется даром! Вызывает недоумение, почему же этот автор и другие не делают следующий, такой очевидный шаг в своих рассуждениях? Конечно же, чтобы инициировать получение мощности потребителем с вала прецессирующего гироскопа необходимо вначале одноактно аккумулировать электрическую энергию в виде кинетической энергии вращения маховика, а затем сколько угодно времени лишь восполнять её малые потери на трение, ведь по теории на производство мощности сил прецессии энергия ротора гироскопа не затрачивается. Для того чтобы подтвердить этот факт, был проведен простой эксперимент. Его цель — проверить, потребляется ли дополнительная электроэнергия мотором гироскопа в процессе утилизации гравитационной энергии на валу прецессии. Для этого мы использовали схему опыта предложенного К.Э.Суорцем. В книге К.Э.Суорца [4] дано изложение начал физики. Там находим описание и трактовку опыта с гироскопом. Цитирую. «Вы можете сделать поразительный образец волчка (или гироскопа) с помощью велосипедного колеса. Подвесьте один конец оси снятого переднего колеса на шнурке, как показано на схеме (рис.3). Отпустите другой конец оси, чтобы колесо поддерживалось только шнурком. Сразу же появляется неуравновешенный момент сил, опрокидывающий колесо. На колесо действует сила тяжести, приложенная к его центру и направленная вертикально вниз. Плечо этой силы равно расстоянию от центра колеса до точки закрепления шнурка. 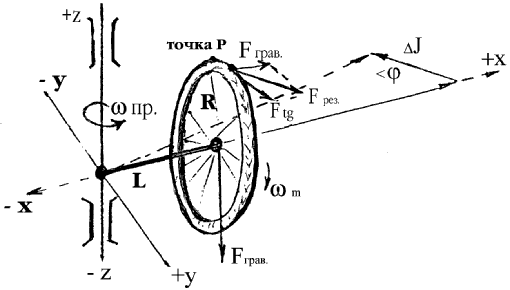 Рис.3. Теперь проделайте то же самое, но на этот раз попросите кого-нибудь раскрутить колесо, прежде чем вы его отпустите. На него по-прежнему будет действовать тот же самый неуравновешенный момент силы тяжести, но колесо не опрокинется и не упадет. Оно останется вертикальным, а его ось будет медленно поворачиваться в горизонтальной плоскости вокруг шнурка. Почему колесо не опрокидывается, и откуда берется момент импульса, связанный с движением его центра по горизонтальной окружности? Для того чтобы объяснить данный феномен, рассмотрим, что происходит с верхней точкой «Р» колеса. Если смотреть сверху, эта часть колеса опрокидывается вправо. Следовательно, действующая на точку Р сила направлена вправо. Однако точка Р при этом быстро движется вперед (когда мы смотрим вниз на колесо). Опрокидывающее усилие сообщает точке Р небольшой импульс (курсив мой, обращает внимание на источник энергии импульса!), направленный вправо, который складывается векторно с основным импульсом этой точки, направленным вперед. Результирующий импульс имеет такое направление, которое соответствует повороту всего колеса направо. Вместо того чтобы опрокинуться, колесо и плоскость его вращения поворачиваются направо. На схеме стрелками, направленными вдоль соответствующих осей, показаны силы и моменты импульса. Наибольшим моментом импульса, направленным вдоль горизонтальной оси, в этой системе обладает вращающееся колесо. Момент силы тяжести также лежит в горизонтальной плоскости, однако он перпендикулярен оси колеса (курсив и жирный шрифт мой). Вследствие этого момент силы тяжести не тормозит колесо, не отбирает его кинетическую энергию вращения для действия момента сил прецессии точки Р! За каждый интервал времени dt момент силы тяжести вызывает изменение момента импульса прецессии точки Р: М · dt = dJ. Это приращение момента импульса направлено перпендикулярно к основному моменту импульса колеса и поэтому не изменяет его модуля. Но момент силы тяжести изменяет направление момента импульса точки Р колеса. Ось колеса поворачивается в горизонтальной плоскости, и этот поворот продолжается все время, пока действует момент силы тяжести. Такой тип движения называется прецессией». В опыте по схеме Суорца ротор в виде велосипедного колеса был заменен цилиндрическим ротором электромотора диаметром 10 см, скоростью вращения в 15 тыс. об\мин и весом около 2 кг. Плечо момента гравитационных сил составило 10 см. На вал прецессии диаметром 1 см был намотан шнур, нагруженный через блок гирей весом 200 г, для того чтобы снимать полезную мощность с вала N = m · g · h / t. В состоянии покоя зафиксированный мотор на максимальных оборотах потреблял постоянный ток напряжением 25 В и силой 0,5 A. Мощность тока составила 12,5 Вт. Угловая скорость вала прецессии составила один оборот за пять секунд. В процессе совершения работы по подъему гири на высоту в 1 м при наматывании шнура на вал прецесии показания амперметра и вольтметра не изменились. То же самое наблюдалось при резком торможении вала прецессии. Также нами были сравнены время полной остановки вращения ротора электродвигателя, находящегося в покое — без всякой нагрузки и с нагрузкой гирей на вал прецессии после отключения питания. В обоих случаях оно составило 31 мин. Кроме того, гироскоп с уже выключенным мотором в течение 17 мин. совершал работу по подъему гири. Вывод: мотор гироскопа в процессе утилизации гравитационной энергии на валу прецессии дополнительной электроэнергии не потреблял! После ознакомления с трактовкой Суоца, Польпера и результатом нашего опыта, становится ясно, что в данном устройстве легко поддерживается константа момента импульса маховика в его основном вращении, так как поддерживать вращение по инерции маховика нужно, лишь преодолевая сопротивление трения качения подшипников, которое с увеличением угловой скорости нарастает лишь линейно (также нам известны конструкции магнитных подвесов, воздушных подшипников и других устройств, сопротивление которых минимально). Увеличение угловой скорости маховика с ее дальнейшим поддержанием необходимо для того, чтобы получить возможность наращивать воздействие внешних сил на ось момента. Силы гравитации могут быть вообще заменены другими консервативными силами, такими, как, например, возвращающие силы пружины или силы, действующие в постоянных магнитах. Так мы можем добиться выработки свободной энергии, намного превышающей потери на трение, путем «съема» мощности сил прецессии с вала гироскопа. Электрическая энергия затрачивается в гироскопе лишь для создания условий действия прецессии. Направив часть полученной свободной энергии на восполнение, мы получим «вечный двигатель второго рода». Сущность получаемого механического эффекта обусловлена природным физическим эффектом, наблюдаемом в гироскопе: взаимосвязью констант двух моментов импульсов вращения — собственно маховика и прецессионного вращения гироскопа, а также эффекта квантования момента импульса прецессии по величине параметра L / R2, где: L — радиус инерции прецессирующей массы маховика и плечо действия гравитационной силы;R — радиус инерции вращения маховика. Другими словами, сила действия гравитации (веса) на плечо при изменении этого параметра каждый раз ограничена пределом константы квантования момента импульса маховика, в котором избыточный инерционный момент (центробежный момент сил инерции) противостоит гравитации, и в котором сохраняется вертикальная плоскость вращения маховика. В этом случае маховик не падает. Объяснение природы процесса получения свободной энергии в прецессионном генераторе. Объяснение природы процесса получения свободной энергии в прецессионном генераторе возможно на базе новой парадигмы физики [5], постулирующей, что элементы вещества есть вихри эфирной среды, находящиеся в состоянии равновесия энергообмена со средой. Эфирная среда (физический вакуум) имеет свойство самоструктурироваться и формировать свои элементы как механические системы (вихри, волновые пакеты стоячих волн) по универсальной кинематической схеме, названной Ивановым Б.П. [6] «организационной формой материи» (ОФМ). Об опыте получения свободной энергии из природного свойства потенциальных полей центробежных сил инерции сообщалось выше и в статьях журнала [2]. Все ОФМ имеют свойства квантово-механических систем: квантование плотности кинетической энергии движения элементов эфира по объему, плотности массы, момента импульса на радиусе кривизны траектории вихря, радиусе инерции локализованной массы элементов эфира. Вечное движение, обмен энергией, ее превращение в среде принимаются новой парадигмой априори и описываются универсальным алгоритмом действия, названным Смирновым А.П. «закон взаимосвязи процессов (ЗВП)» [7]. Это значит, что получение свободной энергии и ее утилизация в технических устройствах представляется возможным. В квантовании плотности кинетической энергии движения элементов эфира по объему в ОФМ, формирующем градиент потенциалов, заключается объяснение механизма образования сил и мощности работы всех потенциальных полей, например, гравитационного поля, электрического, магнитного, при фотоэффекте, в подъемных силах Архимеда и др., в том числе, и образование кинетического момента центробежных сил в потенциальном поле центробежных сил инерции. Кинематическая схема в конструкции гироскопа построена по законам структуры ОФМ и её алгоритма ЗВП. В ней соотношение квантованных моментов импульса прецессии и маховика обеспечивается отношением L / R2. Это соответствует выводам теории Б.П.Иванова: «Стоячий волновой процесс разбивает объем собственного шара ОФМ как внутри ее ядра, так и снаружи на оболочки равной массы материи. По этой причине вследствие уменьшения плотности материи физического поля радиусы оболочек возрастают пропорционально квадратам натурального ряда чисел» [6, стр. 272]. Учет закономерных кинематико-геометрических параметров в конструкции гироскопа и позволяет по принципу ЗВП утилизовать свободную энергию среды, а именно, снять нагрузкой полезную мощность момента сил прецессии на валу гироскопа. Конструкция гироскопа также позволяет пользоваться в устройстве энергией структурной целостности вещества деталей гироскопа, где структурой элементов вещества совершается работа и затрачиваются возвращающие силы упругости вещества (электростатические силы Кулона в кристаллической решетке, силы Ван Дер Вальса), которые постоянно восполняются энергией из пространства эфирной среды. Генератор Маринова-Богомолова (ГМБ)Открытие автором возможности использования свободной энергии при формировании кинетического момента центробежных сил в потенциальном поле центробежных сил инерции позволило создать опытный образец ГМБ. Первое сообщение об изобретении было опубликовано в статье «Российскому изобретателю необходим «технолоджи трансфер» информационно-аналитического бюллетеня «Петербургский Аналитик», №7 от 07.09.1999. В статье сообщалось об открытии метода получения мощности равной около 3 кВт на валу опытного механического устройства, приводимого во вращение электромотором мощностью 8 Вт, что засвидетельствовала в августе 1999 года комиссия в составе представителей Университета Аэрокосмического Приборостроения и редакции журнала «Петербургский Аналитик», возглавляемая профессором Катковым М.С. Данное устройство для получения свободной энергии было названо нами «генератором Маринова — Богомолова» (ГМБ) в память о болгарском ученом и изобретателе Стефане Маринове [8]. В 1998 г. у меня возникла идея реализовать принцип УЭПП, используя систему ультразвуковых резонаторов, перспективных для использования в технических устройствах при получении в массе их вещества не скомпенсированных центробежных сил инерции волновых импульсов. Однако вначале я решил сделать более простую, дешевую механическую модель на пружинных маятниках для лабораторных исследований, удобную для расчетов УЗВ маятников-резонаторов. Из сотрудников Лаборатории Прикладных Проблем Центра Фундаментальных Исследований, созданного доктором В.Я.Брилем при Санкт-Петербургском Горном Университете, в июне 1997 года был организован временный творческий коллектив из семи соавторов. На изготовление экспериментальной установки был заключен договор с фирмой «Отдельное конструкторское бюро ТЕСТ», возглавляемой Б.П.Кузьмин. В марте 1998 г. в процессе испытаний установки нами был получен хороший устойчивый эффект: генерируемая установкой свободная энергия и мощность на выходе превосходила мощность инициации резонанса на два порядка. Мы заключили договор о доработке механической модели до промышленного образца на средства инвестора с фирмой изготовителем «ТЕСТ», однако финансирование прекратилось. Принципиальная схема устройства ГМБ основывается на идее схемы С.Маринова [8] «Генератора Бюллера-Маринова» и частично использует принцип действия известного механизма «центробежный вибратор» и физический эффект прецессии. В этой схеме симметрично и синхронно вращающиеся массы дисбалансов приводят к осциллирующему движению всей системы (корпуса) в пространстве. Аналогичный эффект наблюдается и в родственных механизмах: инерциоидах Толчина и Савелькаева. Отличие нашей схемы (рис.4) от схемы центробежного вибратора состоит в том, что вращательное движение маховиков-дисбалансов было заменено колебательным движением балансирных маятников. Кинематическая схема нашей установки похожа на выше показанную схему Суорца, но построена как система балансирных маятников. Первый балансирный маятник — это подпружиненный рычаг-качели (1), закрепленный на прочном основании, на котором груз (2) колеблется с собственной резонансной частотой на валу отбора мощности (3). Второй балансирный маятник — подсистема, выполняющая роль груза (2) первого. На рычаге (4) маятника колеблется груз (5) 50 кг с собственной резонансной частотой, равной основной частоте первого, но со сдвигом по фазе на четверть периода. 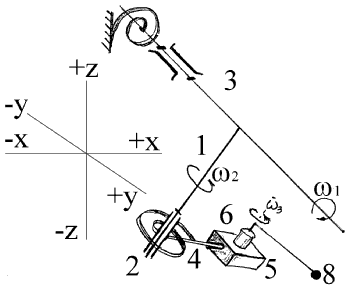 Рис.4. Колебания второго маятника происходят в плоскостях, расположенных ортогонально колебаниям первого, вследствие чего импульс инерционных сил, передаваемый на первый маятник, не «гасит» собственных резонансных колебаний второго. При непосредственном взаимодействии масс под прямым углом (при жестком или мягком соударении масс) обмен скоростью не происходит. Однако в нашей кинематической схеме есть характерная особенность: резонансная подпитка энергией, направленная от второго к первому маятнику, происходит не непосредственно, а опосредствованно, за счет инициированных центробежных сил инерции и энергии деформированной структуры элементов субстанции среды физического вакуума (ФВ, эфира). В результате, осциллирующее движение по инерции всей системы масс в пространстве, переданное на вал качели (3), является причиной приращения мощности устройства. Криволинейные траектории движения масс грузов формируют искусственную систему, потенциальное поле центробежных сил инерции среды ФВ (эфира), которое и совершает работу перемещения грузов маятников в пространстве. Другой источник свободной энергии это — работа сил упругости пружин. Силы эти, в свою очередь, также черпают энергию из среды ФВ в процессе постоянного энергообмена вещества и среды, обеспечивая структурную целостность вещества пружин в пределах меры его прочности (то есть до тех пор, пока сталь не «устанет»). Взаимодействие масс грузов двух маятников в нашей схеме является следствием действия физического эффекта прецессии. Устройство получилось громоздкое, весом более ста килограмм, но дешевое: например, балансирная пружина резонатора была изготовлена из торсионной подвески амортизатора старого автомобиля. Второй балансирный маятник также является автоколебательной системой. Его колебания инициирует и подпитывает (в резонансе) центробежный вибратор, представляющий собой электромотор с редуктором типа «наездник» (8 Вт., 27 В, 6000 об/мин.) (6), вращающий на своем валу рычаг (7) с грузом весом 70 г (8) с угловой частотой около 1 Гц, равной частоте колебаний второго маятника. При частоте вращения груза (8) равной около 1 Гц первый и второй маятники приходят в резонанс, начинают колебаться с максимальной амплитудой через 2 секунды после включения электромотора. Это движение на выходе вала качелей имеет следующую характеристику: колебание вращения на углу 7-10 градусов с частотой около 1 Гц. Выходная мощность, которая регистрировалась путем торможения, была определена равной около 3 КВт. Так как груз (5) 50 кг развивает мощность импульса в 3 КВт за 2 сек, используя мощность инициирующего устройства равную 8 Вт (на два порядка большую), очевидно, что данный прирост мощности не может быть получен за счет аккумуляции в механизме энергии электродвигателя. Для аккумуляции такого количества энергии потребовалось бы более 6 мин. Схема опытного образца ГМБ в настоящее время использована автором в двух других устройствах, расчитанных на массового потребителя. Первое устройство называется «Камертон» и предназначено для обогрева теплиц фермеров и дач горожан. Оно проектируется дешевым по себестоимости и с простым в производстве. Схема данного устройства не приводится, поскольку является «ноу-хау» автора. Еще одна схема — «УЗВ модуль генератор» (рис.5), универсальный генератор электроэнергии. В зависимости от количества модулей в блоке данное устройство может использоваться везде, где есть потребители электроэнергии (бытовые приборы, электромобили, а также заводское оборудование). 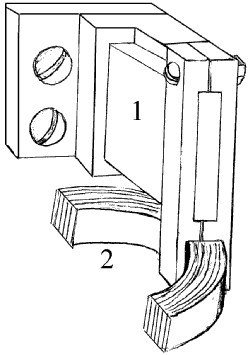 Рис.5. По описанной выше схеме, используя пьезокристаллы для генерации ЭДС (1) и ультразвуковой резонатор (вибратор), например, из пакета никелевых пластин (2), можно построить ГМБ компактный и эффективный. Инициировать колебания собственной частоты резонатора (2) будет соленоид (магнитострикционный эффект), питаемый от генератора переменного тока, подстраиваясь в резонанс по принципу обратной связи в автоколебательных системах. Более подробное описание устройства является «ноу-хау» автора. Таким образом, решающие эксперименты на установках ГБ и ГМБ позволили доказать истинность открытия ПЦСИ, новой парадигмы физики «матрешка» и играют большую роль в борьбе человечества с «энергетическим кризисом».
Литература:
1. Фролов А.В., Статья «Свободная Энергия», Журнал «Новая Энергетика» №1, 2003г.
2. Богомолов В.И., Статьи «Генератор Богомолова», «Эксперимент по использованию свободной энергии», Журналы «Новая Энергетика» №№4,5-6, 2003г.; №1, 2004.
3. Пельпер С.П., «Гироскопические приборы и автопилоты», М.: Наука, 1964г., стр.32-33.
4. Суорц Кл.Э. «Необыкновенная физика обыкновенных явлений». — Пер. с англ., М.: Наука. Гл. ред. физ.-мат. лит., 1986, стр.174-175.
5. Богомолов В.И. «Парадигма физической картины мира «матрёшка». Принципиальная схема утилизации энергии консервативных полей», сборник МАИСУ (Международной Академии «Информация, связь, управление в технике, природе, обществе») за 2002 г.: «Проблемы космической безопасности», — СПб., 2002.
6. Иванов Б.П. «Физическая модель Вселенной». — СПб.: Политехника, 2000.
7. Смирнов А.П. «Физика реальности», сборник «Принцип Порядка», А.П.Смирнов, И.В. Прохорцев, — СПб, ЗАО «ПиК», 2002.
8. Маринов С. «Использование инерциальных сил для производства свободной энергии» в сборнике «Проблемы пространства, времени, тяготения», сборник научных статей по материалам IV Международной конференции 16-21 сентября 1996 г., Санкт-Петербург, Политехника СПб, 1997.
9. Басин М.А. «Компьютеры. Вихри. Резонансы. (Волновая теория взаимодействия структур и систем)» — Часть2 — СПб.: Норма, 2002. ♦
Источник: http://khd2.narod.ru/authors/bgmlv/rprt04.htm |












